machine code read this before 17/feb/2011

machine code link

Binary 2's complement
Binary Numbers in 60 Seconds
computer chips

binary and all that

www.theteacher.info/webpages/textbook/OCRnum.pdf

To be completed by 8/2/2011

6

Question 4

Create a folder/directoryQuestion4 for your new program.

The variable table, Table 2, and the Structured English algorithm describe a simplified

version of the Guess the Word/Phrase Game.

Table 2

Identifier                  Data Type        Purpose

NewWord               String               Stores the setter’s word to be guessed

UserWordGuess      String               Stores a word that is the user’s guess

OUTPUT "The new word?"
INPUT NewWord
OUTPUT "Your guess?"
INPUT UserWordGuess
IF UserWordGuess IS EQUAL TO NewWord

THEN OUTPUT "CORRECT"

ELSE OUTPUT "INCORRECT"

ENDIF

What you need to do

Write a program for the above algorithm in the programming language of your choice.

Test the program as follows.

Test 1:Input of the new word EAGLE followed by a correct guess.

Test 2:Input of the new word BEAR followed by an incorrect guess.

Save the program source code and screen shots of test in blog

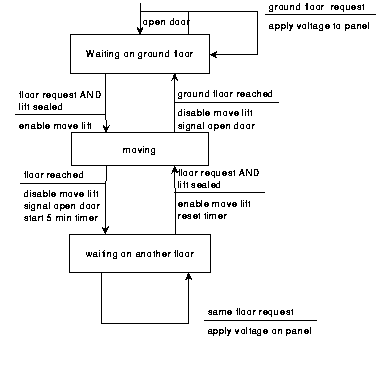
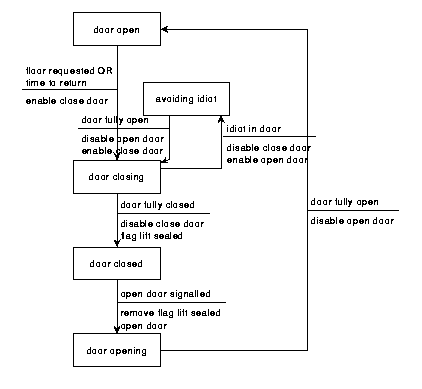
State Transition Diagrams (STD's)

menu: home , si-daq

State Transition Diagrams (STD's)

An STD  is a way of describing the time-dependent behaviour of a system. The basic consistency rule is: "A system's behaviour in any state must be the same no matter by which path the state is arrived at".
States:

• A state is an observable mode of behaviour of the system.
• At any time a particular STD can only be in one state.
• .. but a system's behaviour could be described by more than one state transition diagram

Transition conditions:

• internal events or events external to the system

Transition actions:

• actions in response to the events
• triggering one-shot actions
• synchronizing between different STD's
• producing control outputs

Drawing STD's:

• Identify observable states of the system
• Select the states with normal behaviour
• Specify the conditions that mark a transition
• Specify the actions to produce the observable behaviour in the destination state for each transition
• If the system is complex, partition the diagram in several STD's

The classical elevator example:

• just one lift
• one floor can be requested at a time
• no call buttons on any floors
• the lift waits at the requested floor for five minutes if no-one selects a floor. Then it returns to the ground floor.
• There is a photocell protection on the doors
• The lift will not move with the doors open

STD's:

Converting Decimal Fractions to Binary

Converting Decimal Fractions to Binary

In the text proper, we saw how to convert the decimal number 14.75 to a binary representation. In this instance, we "eyeballed" the fractional part of the binary expansion; 3/4 is obviously 1/2 + 1/4. While this worked for this particular example, we'll need a more systematic approach for less obvious cases.
In fact, there is a simple, step-by-step method for computing the binary expansion on the right-hand side of the point. We will illustrate the method by converting the decimal value .625 to a binary representation..
Step 1: Begin with the decimal fraction and multiply by 2. The whole number part of the result is the first binary digit to the right of the point.

Because .625 x 2 = 1.25, the first binary digit to the right of the point is a 1.
So far, we have .625 = .1??? . . . (base 2) .

Step 2: Next we disregard the whole number part of the previous result (the 1 in this case) and multiply by 2 once again. The whole number part of this new result is the second binary digit to the right of the point. We will continue this process until we get a zero as our decimal part or until we recognize an infinite repeating pattern.

Because .25 x 2 = 0.50, the second binary digit to the right of the point is a 0.
So far, we have .625 = .10?? . . . (base 2) .

Step 3: Disregarding the whole number part of the previous result (this result was .50 so there actually is no whole number part to disregard in this case), we multiply by 2 once again. The whole number part of the result is now the next binary digit to the right of the point.

Because .50 x 2 = 1.00, the third binary digit to the right of the point is a 1.
So now we have .625 = .101?? . . . (base 2) .

Step 4: In fact, we do not need a Step 4. We are finished in Step 3, because we had 0 as the fractional part of our result there.

Hence the representation of .625 = .101 (base 2) .

You should double-check our result by expanding the binary representation.

Infinite Binary Fractions

The method we just explored can be used to demonstrate how some decimal fractions will produce infinite binary fraction expansions. We illustrate by using that method to see that the binary representation of the decimal fraction 1/10 is, in fact, infinite.
Recall our step-by-step process for performing this conversion.
Step 1: Begin with the decimal fraction and multiply by 2. The whole number part of the result is the first binary digit to the right of the point.

Because .1 x 2 = 0.2, the first binary digit to the right of the point is a 0.
So far, we have .1 (decimal) = .0??? . . . (base 2) .

Step 2: Next we disregard the whole number part of the previous result (0 in this case) and multiply by 2 once again. The whole number part of this new result is the second binary digit to the right of the point. We will continue this process until we get a zero as our decimal part or until we recognize an infinite repeating pattern.

Because .2 x 2 = 0.4, the second binary digit to the right of the point is also a 0.
So far, we have .1 (decimal) = .00?? . . . (base 2) .

Step 3: Disregarding the whole number part of the previous result (again a 0), we multiply by 2 once again. The whole number part of the result is now the next binary digit to the right of the point.

Because .4 x 2 = 0.8, the third binary digit to the right of the point is also a 0.
So now we have .1 (decimal) = .000?? . . . (base 2) .

Step 4: We multiply by 2 once again, disregarding the whole number part of the previous result (again a 0 in this case).

Because .8 x 2 = 1.6, the fourth binary digit to the right of the point is a 1.
So now we have .1 (decimal) = .0001?? . . . (base 2) .

Step 5: We multiply by 2 once again, disregarding the whole number part of the previous result (a 1 in this case).

Because .6 x 2 = 1.2, the fifth binary digit to the right of the point is a 1.
So now we have .1 (decimal) = .00011?? . . . (base 2) .

Step 6: We multiply by 2 once again, disregarding the whole number part of the previous result. Let's make an important observation here. Notice that this next step to be performed (multiply 2. x 2) is exactly the same action we had in step 2. We are then bound to repeat steps 2-5, then return to Step 2 again indefinitely. In other words, we will never get a 0 as the decimal fraction part of our result. Instead we will just cycle through steps 2-5 forever. This means we will obtain the sequence of digits generated in steps 2-5, namely 0011, over and over. Hence, the final binary representation will be.

.1 (decimal) = .00011001100110011 . . . (base 2) .

The repeating pattern is more obvious if we highlight it in color as below:

.1 (decimal) = .00011001100110011 . . . (base 2) .

2's Complement Representation for Signed Integers

Question 2

2's Complement Representation for Signed Integers

Definition Calculation of 2's Complement Addition Subtraction Multiplication Division Sign Extension Other Signed Representations Notes

---

Definition

Property

Two's complement representation allows the use of binary arithmetic operations on signed integers, yielding the correct 2's complement results.

Positive Numbers

Positive 2's complement numbers are represented as the simple binary.

Negative Numbers

Negative 2's complement numbers are represented as the binary number that when added to a positive number of the same magnitude equals zero.

Integer		2's Complement
Signed	Unsigned
5	5	0000 0101
4	4	0000 0100
3	3	0000 0011
2	2	0000 0010
1	1	0000 0001
0	0	0000 0000
-1	255	1111 1111
-2	254	1111 1110
-3	253	1111 1101
-4	252	1111 1100
-5	251	1111 1011

Note:  The most significant (leftmost) bit indicates the sign of the integer; therefore it is sometimes called the sign bit.

If the sign bit is zero,

then the number is greater than or equal to zero, or positive.

If the sign bit is one,

then the number is less than zero, or negative.

Calculation of 2's Complement

To calculate the 2's complement of an integer, invert the binary equivalent of the number by changing all of the ones to zeroes and all of the zeroes to ones (also called 1's complement), and then add one.
For example,

0001 0001(binary 17)      1110 1111(two's complement -17)
NOT(0001 0001)	=	1110 1110  (Invert bits)
1110 1110 + 0000 0001	=	1110 1111  (Add 1)

2's Complement Addition

Two's complement addition follows the same rules as binary addition.
For example,

5 + (-3)  =  2		0000 0101	=	+5
		+ 1111 1101	=	-3
		0000 0010	=	+2

2's Complement Subtraction

Two's complement subtraction is the binary addition of the minuend to the 2's complement of the subtrahend (adding a negative number is the same as subtracting a positive one).
For example,

7 - 12  =  (-5)		0000 0111	=	+7
		+ 1111 0100	=	-12
		1111 1011	=	-5

2's Complement Multiplication

Two's complement multiplication follows the same rules as binary multiplication.
For example,

(-4) × 4  =  (-16)		1111 1100	=	-4
		× 0000 0100	=	+4
		1111 0000	=	-16

2's Complement Division

Two's complement division is repeated 2's complement subtraction. The 2's complement of the divisor is calculated, then added to the dividend. For the next subtraction cycle, the quotient replaces the dividend. This repeats until the quotient is too small for subtraction or is zero, then it becomes the remainder. The final answer is the total of subtraction cycles plus the remainder.
For example,

7 ÷ 3  =  2 remainder 1		0000 0111	=	+7		0000 0100	=	+4
		+ 1111 1101	=	-3		+ 1111 1101	=	-3
		0000 0100	=	+4		0000 0001	=	+1 (remainder)

Sign Extension

To extend a signed integer from 8 bits to 16 bits or from 16 bits to 32 bits, append additional bits on the left side of the number. Fill each extra bit with the value of the smaller number's most significant bit (the sign bit).
For example,

Signed Integer	8-bit Representation	16-bit Representation
-1	1111 1111	1111 1111 1111 1111
+1	0000 0001	0000 0000 0000 0001

Other Representations of Signed Integers

Sign-Magnitude Representation

Another method of representing negative numbers is sign-magnitude. Sign-magnitude representation also uses the most significant bit of the number to indicate the sign. A negative number is the 7-bit binary representation of the positive number with the most significant bit set to one. The drawbacks to using this method for arithmetic computation are that a different set of rules are required and that zero can have two representations (+0, 0000 0000 and -0, 1000 0000).

 

Offset Binary Representation

A third method for representing signed numbers is offset binary. Begin calculating a offset binary code by assigning half of the largest possible number as the zero value. A positive integer is the absolute value added to the zero number and a negative integer is subtracted. Offset binary is popular in A/D and D/A conversions, but it is still awkward for arithmetic computation.

 

For example,

Largest value for 8-bit integer  =  28  =  256

Offset binary zero value  =  256  ÷  2  =  128(decimal)  =  1000 0000(binary)

1000 0000(offset binary 0) + 0001 0110(binary 22) = 1001 0110(offset binary +22)

1000 0000(offset binary 0) - 0000 0111(binary 7) = 0111 1001(offset binary -7)

Signed Integer	Sign Magnitude	Offset Binary
+5	0000 0101	1000 0101
+4	0000 0100	1000 0100
+3	0000 0011	1000 0011
+2	0000 0010	1000 0010
+1	0000 0001	1000 0001
0	0000 0000 1000 0000	1000 0000
-1	1000 0001	0111 1111
-2	1000 0010	0111 1110
-3	1000 0011	0111 1101
-4	1000 0100	0111 1100
-5	1000 0101	0111 1011

Notes

Other Complements

1's Complement  =  NOT(n)  =  1111 1111 - n

9's Complement  =  9999 9999 - n

10's Complement  =  (9999 9999 - n) + 1

 

Binary Arithmetic

Addition

Subtraction

Multiplication

Division

Computer programs process and store numeric data.

A computer game stores the following data:

•

level of difficulty as an integer in the range 1 to 15

•

player rating as an integer in the range -120 to +120

•

fuel level as a number with a fractional part.

This number is in the range 0 to 100

0 8

The level of difficulty is stored as an unsigned binary number using a single byte.

For a particular game, the level of difficulty was set at 11.

Calculate its binary value.

1011

Use the grid for rough working, then copy the bit pattern to your

Electronic Answer Document.

(2 marks)

0 9

A player rating value is stored as a two’s complement integer using a single byte.

Convert the player rating value of 119 into binary

Converting to binary ...
119/128 = 0
119/64 = 1
55/32 = 1
23/16 = 1
7/8 = 0
7/4 = 1
3/2 = 1
1/1 = 1
Final Answer=01110111



-13 2's compliment      11110011

1.4 Representation of data in computer systems

1.4 Representation of data in computer systems

Images

Candidates should be able to:

11. explain the representation of an image as a series of pixels represented in binary
12. explain the need for metadata to be included in the file such as height, width and colour depth
13. discuss the effect of colour depth and resolution on the size of an image file.

Questions

How can an image be represented in binary?
Bitmap images:
Bitmap images are made up of individual pixels and the colour of each pixel is stored as a binary code. The whole image is therefore stored as a series of binary numbers.
If more memory bits are used to represent each pixel then more combinations of binary numbers are possible so more colours are possible in the image.
In the example on the right the animation zooms into the small image to show the individual pixels. The image has a 1 bit colour depth because only 1 bit is used for each pixel, giving 2 possible colours, in this case black and white. The binary code for each pixel is therefore simply 1 or 0.

Vector images:

Vector images store information as mathematical instructions rather than as individual pixels. For example, to draw a vector circle the software only needs to store the coordinates of the circle centre, the radius, the line thickness, style and colour, the fill type and colour(s) and the image scale.
This information would be stored using binary codes for the instructions. The result is that the file size of a vector image would be considerably smaller than the equivalent bitmap image which would need to store the information for every pixel in the image, including the area outside the circle.
Although vector images can have graduated fills these are mathematically defined and vector images cannot represent the level of detail needed for photographic images.
As well as the smaller file sizes, vector images have the advantage that they can be scaled to any size without any loss of detail or pixilation as would occur with a bitmap image. Also, if a vector image was scaled-up and then saved it would have the same file size as the original.

---

Why does metadata need to be included in an image file?
Metadata is needed in a bitmap image file because the software that displays an image needs to know:

• The height and width of the image - so each line of the image starts in the right place.
• The resolution depth - so the image displays at the correct size.
• The colour depth  - so the correct number of bits are used to represent each pixel.

An image with  the CORRECT colour depth metadata - 1 bit colour depth	The same data but the WRONG colour depth metadata - 2 bit colour depth

An image with the CORRECT size metadata - 16 x 24 pixels	The same data but with the WRONG size metadata - 24 x 16 pixels
	The original image, before zooming  in to reveal the individual pixels.

NOTE: An image file may also contain metadata describing the type and amount of compression in the image, the software used to create the file and, if it is a digital photograph, the date and time the image was taken and the camera/lens settings.

---

What is colour depth and how does it effect the size of an image file?

Colour depth in bits (n)	Number of possible colours (2n)	Example binary code(s) used to  store the colour information about each pixel
1	2	0, 1
2	4	00, 01, 10, 11
3	8	000, 001, 111 etc.
4	14	0000, 0001, 1110 etc.
8	256	10010101, 11101101 etc.
24	16,777,216	010110101110001101001101

Colour depth describes the number of bits of memory that are used to store the colour information about each pixel in a bitmap image.
With 1 bit colour depth the number of bits used to store the information about each pixel is 1. This allows 2 colours, represented by 0 or 1.
With 3 bit colour depth the number of bits used to store the information about each pixel is 3. This allows 8 colours, represented by the binary codes 000, 001, 010, 011, 100, 101, 110 and 111.
SUMMARY: The greater the colour depth of a bitmap image, the greater the file size because more memory is used to store the colour data about each pixel.

Colour mapping, palette tables and Direct colour:

Colour mapping - With low colour depths (up to 8 bit) it is practical to map every colour to a binary code because there are not too many colours involved. This is called colour mapping and an example might be the binary code 110 representing yellow.
Palette tables - The GIF file format uses 8 bits for each pixel so it can display 256 different colours. However, every GIF image can have a different set of 256 colours because they are stored as part of the file in a palette table. This table stores each of the 256 colours using 24 bit direct colour so there are 16,777,216 possibilities. Each of the 256 colours in the palette is indexed using 8 bits so it is the index value that is actually stored for each pixel in a GIF file.
Direct colour - As the colour depth increases colour mapping and palettes become impractical due to the number of simultaneous colours that the image can display. In higher colour depths (8 bit and above) a system called direct colour is therefore used. In this the bits allocated to each pixel directly encodes the relative brightness of Red, Green and Blue to specify what is called an RGB colour. For example, if 24 bit direct colour was used then the code for a yellow pixel (maximum red and green and zero blue) would be;

• 255, 255, 0 in denary
• 111111111111111100000000 in binary (note the use of 24 bits)
• FFFF00 in hexadecimal

EXPANSION TOPIC - Colour mapping and Direct colour

---

What is resolution depth and how does it effect the size of an image file?
Resolution depth is a measure of how much detail there is in an image. A detailed image can be magnified and still stay sharp.
In a bitmap image this depends on the pixel density, the number of pixels per unit of distance (not the total number of pixels in the image).
The resolution depth of a screen image is usually measured in pixels per inch (PPI). A low resolution image of an object will appear smaller on screen and will become pixelated (the individual pixels will be clearly visible) when it is magnified to the same size as a high resolution image of the same object.
To physically reduce the size of a bitmap image it can be resampled. This results in a smaller file size as pixels are discarded and the image therefore appears smaller on the screen. If it is then magnified back to the original size it will appear pixelated.
NOTE: Although resampling is usually thought of as reducing the resolution this is only true if the print size is kept constant. An image resampled in this way would lack the detail of the original when it was printed out. It is equally possible to resample an image by reducing the print size and keeping the resolution constant. In this case the printed image would still appear sharp but be smaller.
Just decreasing the resolution, without resampling the image, makes no change to the image on the screen but produces a larger printed image (there are still the same number of pixels to print out but if the PPI is lower then 1 inch of printing will have printed less of them)
SUMMARY: A high resolution bitmap image will have a greater the file size than the equivalent low resolution image because more memory is used to store the colour data of the extra pixels.
NOTE: Because vector images are only stored as a set of mathematical instructions, halving the size of a vector image would effectively make no difference to the file size. However, halving the size of a bitmap image would effectively make the file size 1/4 of the original.

Vector Graphics explained

In the world of graphic creations there are two central forms of graphics. Option one is Vector graphics or the other form of raster (Bitmap) graphics. There are some chief differences among the two formats, and it is important to understand the differences among the two, in order to be aware of what time which of the two would be most beneficial. This informational text will focus on the vector graphics format.

Vector graphics, graphic image format created through applications such as, Adobe Illustrator. These programs are occasionally referred to as a drawing application. The vector graphic format does not use pixels. The vector graphic format will record a explicit coordinate inside a file as a reference point, will then in turn record all other information needed, for example, line gradients, and the thickness of a formula. What this encompasses, when editing a file there are no pixels to edit on the screen, instead there is an adding to and altering of the formula's information. For this reason, vector graphics are entirely scalable. Regardless of the size the item appears on the screen, the size will not determines the depth of largeness the file size of the image will be. Vector graphic images are available in a large range of various file types; it will ultimately depend on the initial application that created them. The standard formats include EPS, AI, CDR, or SVG.

Vector graphics are more suitable for sketching images from scratch. For example, if you are creating a logo from scratch or sketching a character with a cartoon style, then these types of graphics may be suitable. Either of these projects would have usable advantage due to the scalability in vector graphic applications, as well as, the other available tools the vector applications have access to, designed exclusively for help with drawing projects.

Vector is a term that in describes the available use of geometrical primitives that are based on mathematical equations for representation of computer graphics; the format includes basics such as shapes and points. It is a re-sizable style of artwork without the worry of resolution and/or quality of picture. The program allows the designer to take a minimal size logo and increase its size to that of a billboard , without the logo losing any of the original detail.

Vector artwork is the most popular use in logo design for products designed for promotional use. Vector artwork allows the designer to imprint a company's logo onto another project, as it will be consistent in style design.


Read more: http://www.articlesbase.com/branding-articles/vector-graphics-explained-1820423.html#ixzz1CtzdUzqf
Under Creative Commons License: Attribution

The pixel

A Beginners Guide to Bitmaps

Written by Paul Bourke
Renderings and models by Peter Diprose and Bill Rattenbury
November 1993

---

Introduction

This document is to serve as an elementary introduction to bitmaps as they are used in computer graphics.

Definition

Bitmaps are defined as a regular rectangular mesh of cells called pixels, each pixel containing a colour value. They are characterised by only two parameters, the number of pixels and the information content (colour depth) per pixel. There are other attributes that are applied to bitmaps but they are derivations of these two fundamental parameters.

Note that bitmaps are always orientated horizontally and vertically. Pixels should be considered square although they may have other aspect ratios in practice.
In the majority of situations bitmaps are used to represent images on the computer. For example the following is a bitmap which has 397 pixels horizontally, 294 pixels vertically, and each pixel contains a grey value from a possible 256 different greys.

Each pixel in a bitmap contains certain information, usually interpreted as colour information. The information content is always the same for all the pixels in a particular bitmap. The amount of colour information could be whatever the application requires but there are some standards, the main ones are described below.

1 bit (black and white)

This is the smallest possible information content that can be held for each pixel. The resulting bitmap is refered to as monochrome or black and white. The pixels with a 0 are refered to as black, pixels with a 1 are refered to as white. Note that while only two states are possible they could be interpreted as any two colours, 0 is mapped to one colour, 1 is mapped to another colour.

8 bit greys

In this case each pixel takes 1 byte (8 bits) of storage resulting in 256 different states. If these states are mapped onto a ramp of greys from black to white the bitmap is refered to as a greyscale image. By convention 0 is normally black and 255 white. The grey levels are the numbers in between, for example, in a linear scale 127 would be a 50% grey level.

In any particular application the range of grey values can be anything, it is most common to map the levels 0-255 onto a 0-1 scale but some programs will map it onto a 0-65535 scale (see Apples colour specification system as an example).

24 bit RGB

This is the next step from 8 bit grey, now there is 8 bits allocated to each red, green, and blue component. In each component the value of 0 refers to no contribution of that colour, 255 refers to fully saturated contribution of that colour. Since each component has 256 different states there are a total of 16777216 possible colours.

This idea of RGB colour space is a fundamental concept in computer graphics. In RGB space any colour is represented as a point inside a colour cube with orthogonal axes r,g,b.

Note that grey values form a straight line from black to white along the diagonal of the cube, r = g = b.

8 bit indexed colour

Indexed colour is a more economical way of storing colour bitmaps without using 3 bytes per pixel. As with 8 bit grey bitmaps each pixel has one byte associated with it only now the value in that byte is no longer a colour value but an index into a table of colours, called a palette or colour table.

There are a number of interesting attributes of such a colour indexing system. If there are less than 256 colours in the image then this bitmap will be the same quality as a 24 bit bitmap but it can be stored with one third the data. Interesting colouring and animation effects can be achieved by simply modifying the palette, this immediately changes the appearance of the bitmap and with careful design can lead to intentional changes in the visual appearance of the bitmap.

A common operation that reduces the size of large 24 bit bitmaps is to convert them to indexed colour with an optimised palette, that is, a palette which best represents the colours available in the bitmap.

4 bit indexed colour

This is identical to 8 bit colour except now only half a byte, 4 bits are used for the index. This supports a table of up to 16 colours.

32 bit RGB

This is normally the same as 24 bit colour but with an extra 8 bit bitmap known as an alpha channel. This channel can be used to create masked areas or represent transparency.

16 bit RGB

This is generally a direct system with 5 bits per colour component and a 1 bit alpha channel.

Resolution

Resolution is an attribute of a bitmap that is necessary when visually viewing or printing bitmaps because pixels by themselves have no explicit dimensions. Resolution is normally specified in pixels per inch but could be in terms of any other unit of measure. Most printing processes retain the pixels per inch (DPI) units for historical reasons. On devices with nn rectangular pixels the resolution may be specified as two numbers, the horizontal and vertical resolution.

The concept of resolution being independent of the information content of a bitmap is very important, given a constant colour depth then the information content between different bitmaps is only related to the number of pixels vertically and horizontally. The quality however, when the bitmap is displayed or printed does depend on the resolution. Since the resolution determines the size of a pixel it can also be used to modify the size of the overall image.

As an example consider one bitmap which is 200 pixels horizontally and 100 pixels vertically. If this bitmap was printed at 100DPI then it would measure 2 inches by 1 inch. If however the same bitmap was printed at 200 DPI then it would only measure 1 inch by half an inch.

Whenever a bitmap is displayed on a computer monitor resolution need to be considered. Most computer monitors have a range of resolution from 60DPI at the low resolution end to 120DPI for high resolution displays. As with printed matter the higher the resolution the less apparent the pixel nature of the bitmap will be.

As a further example the following two images are identical in information content, they do however have different resolutions and hence different pixel sizes. The smaller is 80DPI and the larger is 30DPI. The pixels are much more evident in the larger version.

This is not the whole story when it comes to representing bitmaps on physical devices because different devices have different colour depth capabilities.

Colour depth conversion.

Very often it is necessary to represent a bitmap with one colour depth onto a device with different colour depth capabilities. Of course if the destination device has better colour than the bitmap then there is no issue since the bitmap can be exactly represented. In the reverse situation where the destination has different and lower capabilities, then the bitmap has to be converted into something that gives the best possible representation.

As an example consider the problem of representing greyscale images on monochrome (black and white) devices. This is achieved by using a variable number of black and white pixels to represent a grey level. Fortunately the black and white device usually has much higher resolution than the bitmap so there are a number of pixels available to create the greyscale approximation. Consider a 75DPI greyscale bitmap to be displayed on a 300DPI black and white printer. There is a matrix of 4x4 black and white pixels that can be used to represent each greyscale pixel.

There are a number of techniques that can be used to form the corresponding arrangement of black and white pixels, one technique is called dithering. Even using dithering there are lots of possible algorithms for deciding the dithered pixel arrangement. The following shows a grey level ramp with the corresponding black and white dithered examples (greatly enlarged) using pattern and diffusion dithering.

As already mentioned there are other methods of converting bitmaps of high colour depth into those of lower colour depth but higher resolution, on such technique used in the printing industry is called screening. Screening will not be discussed here except to say that it approximates grey levels by different size objects (the size of the object is proportional to the grey level) The objects are arranged on in a regular matrix which is at some angle to the horizontal. The most commonly used imaging objects are dots, lines and rectangles. The following shows a grey level ramp with the corresponding black and white screened examples (greatly enlarged) using dot and line screens.

The above discussion and examples of colour depth conversion have been made with respect to greyscale images. Converting high colour depth images to low colour depth representations is no different in concept, generally the process is just done three times, one for each colour component.

Bitmap Storage

The most straightforward way of storing a bitmap is simply to list the bitmap information, byte after byte, row by row. Files stored by this method are often called RAW files. The amount of disk storage required for any bitmap is easy to calculate given the bitmap dimensions (N x M) and colour depth in bits (B). The formula for the file size in KBytes is

where N and M are the number of horizontal and vertical pixels, B is the number of bits per pixel. The following table shows the file sizes of a few bitmap types if they are stored in RAW format.

image dimensions     colour depth     file size
    128 x 128             1 bit            2 KB
                          8 bits          16 KB
                         24 bits          48 KB
    256 x 256             1 bit            8 KB
                          8 bits          64 KB
                         24 bits         192 KB
     1K x 1K              1 bit          128 KB
                          8 bits           1 MB
                         24 bits           3 MB

As can be seen from this table, large 24bit images will result in very large files, this is why compression becomes important. There are a large number of file formats used for storing compressed bitmaps from the trival to the very complicated. The complicated formats exist because of the very large bitmap files that would exist if compression was not used. There are two broad categories of compressed file format, those which are lossless (retain the bitmaps perfectly) and those which are lossy. The following shows the main heirarchy of compression techniques.

The crudest way of reducing the size of bitmap files is to reduce the colour information, this is called bit reduction or quantization. For example one could convert 24 bit bitmaps to 8 bit indexed bitmaps using dithering to simulate the lost colours. The most common lossy format by far is JPEG, a description of how it works is well outside the scope of this discussion. Its main advantage is that it can offer vastly better compression ratios than the lossless formats. For example consider the following bitmap the original of which is 500 x 350 pixels at 24 bit colour. Using the formula given earlier the uncompressed file size is 500 x 350 x 24 / 8 / 1024 = 513K

Saved in greyscale (bit depth reduction) the file is 171K (3 times smaller), saved and compressed using RLE it is 388K (75% of the original), saved using LZW compression it is 188K (36% of the original), saved as JPEG it is 30K (a compression ratio of 17:1).
The following is a description of the simplest lossless compression technique called run length encoding (RLE) that is used with good effect for bitmaps with only a few colours. Consider the following small, 17 x 10 pixel, 8 bit image. RLE than described here this is the basic principle behind run length encoding. In order for RLE to achieve some degree of compression there needs to be runs of the same colour, for this reason it is unlikely to be useful for highly coloured images such as 24 bit photographs.

If this was to be stored in RAW form it would need 16 bytes per row for all 10 rows. However the first two rows are all the same level so it is more efficient to simply save the number of same colours in a run along with the run colour. The first two rows instead of needing 16 bytes only need 2 bytes each.

In raw format the first three rows would be

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0

Using run length encoding the first three rows would be

16 0
 16 0
 2 0 12 1 2 0

While there are more details involved in actual implementations of

Specific formats

The following is a list and brief comments of some specific file formats that are widely used for saving bitmaps.

Format: TIFF (Tagged Image FIle Format)
Platforms: Commonly supported on Mac/DOS-WINDOWS/Unix
Owner: Aldus
Notes: TIFF is an international standard for storing and interchanging bitmaps between applications and hardware platforms. It is almost always supported by major applications that provide bitmap manipulation. The format consists of items called tags which are defined by the standard. Each tag is followed by a tag dependent data structure. Supports most colour spaces and compression methods.

Format: PCX
Platforms: Primarily DOS-WINDOWS
Owner: ZSoft Corp
Notes: The oldest and most commonly supported format on DOS machines. Can support indexed or full 24 bit colour. Run length encoding only.

Format: GIF
Platforms: Commonly supported on Mac/DOS-WINDOWS/Unix
Owner: CompuServe
Notes: GIF is a rather underfeatured but quite popular format. It is used the most on bulletin boards and on the worldwide internet. It is limited to 8 bit indexed colour and uses LZW compression. Can include multiple images and text overlays. Also contains support for layers and animation.

Format: PICT
Platforms: Exclusively Mac
Owner: Apple
Notes: PICT is a Macintosh only format, indeed it is virtually impossible for it to exist on any machine but the Macintosh. The interpretation of a PICT is handled by the Macintosh operating system and thus is supported by almost all Macintosh applications. This format is responsible for the successful transfer of image data on the Macintosh and is used in cut/copy/paste operations. Supports most colour spaces and compression methods including JPEG.

Format: PNG (Portable Network Graphics)
Platforms: Commonly supported on Mac/DOS-WINDOWS/Unix
Owner: None, patent free
Notes: Very powerful format which slowly seems to be adopted for the WWW. Supports colour upto 48 bits, grey upto 16 bits. Supports multiple compression schemes and bit depths including user defined ones.

Format: RAW
Platforms: Any
Owner: None
Notes: This is the simplest of all ways to store images, just as "raw" bytes. For example one byte per pixel for grey scale or 3 bytes per pixel for RGB color. There is no standard header and so even the size of the image needs to be specified for programs that might read the image.

Format: PPM (Portable PixMap)
Platforms: Any, originally UNIX
Owner: None
Notes: This is little more than the raw format with a few semi-agreed upon header fields. Typically used for 8 bit grey or 24 bit RGB colour. images.

Format: GEM
Platforms: Almost exclusively DOS/Atari
Owner: Digital Research
Notes: Supported by GEM operating system.

Format: IFF/ILBM
Platforms: Almost exclusively Amiga
Owner: Electronic Arts
Notes: Supports four bit colour map and 24 bit direct colour.

Format: TARGA
Platforms: Mixed support on Mac/DOS-WINDOWS/UNIX
Owner: TrueVision Inc
Notes: Originally designed for VISTA data capture boards. Little more than a RAW format with some extra header information.

Format: BMP/DIB
Platforms: Primarily DOS-Windows
Owner: MicroSoft
Notes: MicroSoft Windows format, rarely supported elsewhere. Supports 1,2,4,8, and 32 bit colour images.

Format: Sun raster
Platforms: Primarily Sun
Owner: Sum MicroSystems
Notes: Only supported by Sun. Use RLE and either 8 bit greyscale or 24/32 bit colour.

Format: XBM
Platforms: Primarily X systems
Owner: MIT X Corp
Notes: Specifically for X windows system bitmap routines, used for cursors and icons.

Format: XWD
Platforms: Primarily X systems
Owner: MIT X Corp
Notes: Screen save format under X windows. Implements black and white through to 24 bit direct colour.

Colour "depth"

Comp examination paper

http://www.scribd.com/doc/31307156/AQA-COMP1-W-QP-JUN09http://www.scribd.com/doc/31307156/AQA-COMP1-W-QP-JUN09

description of Comp 1 and Comp 2

Unit 1 – COMP1
Problem Solving, Programming, Data Representation and
Practical Exercise
60% of AS, 30% of A Level
2 hour on-screen examination
100 marks
Preliminary Material (comprising Instructions to Candidates), the Skeleton
Program (in each of the available programming languages) and, if appropriate,
test data for use in the examination will be released on 1 March on e-AQA1 only
with the Electronic Answer Document.
Centres may release the above mentioned materials to their candidates at any
time on or after 1 March, subject to the instructions given in the Teachers’ Notes.
CanUnit 1 – COMP1
Problem Solving, Programming, Data Representation and
Practical Exercise
60% of AS, 30% of A Level
2 hour on-screen examination
100 marks
Preliminary Material (comprising Instructions to Candidates), the Skeleton
Program (in each of the available programming languages) and, if appropriate,
test data for use in the examination will be released on 1 March on e-AQA1 only
with the Electronic Answer Document.
Centres may release the above mentioned materials to their candidates at any
time on or after 1 March, subject to the instructions given in the Teachers’ Notes.
Candidates must use the examination materials to answer short questions and to
write a program in the examination.
Teachers’ Notes will also be released on 1 March on e-AQA only.
Available in June only

Unit 2 – COMP2
Computer Components, The Stored Program Concept and The Internet
40% of AS, 20% of A Level
1 hour written examination
60 marks
Compulsory short answer questions.
Available January and June
didates must use the examination materials to answer short questions and to
write a program in the examination.
Teachers’ Notes will also be released on 1 March on e-AQA only.
Available in June only
  
 
Unit 2 – COMP2
Computer Components, The Stored Program Concept and The Internet
40% of AS, 20% of A Level
1 hour written examination
60 marks
Compulsory short answer questions.
Available January and June

converting between bases

Introduction to decimal, binary, hexadecimal, octal and converting between bases

Decimal

We count in what is called the decimal counting system. Decimal has 10 digits which are 0,1,2,3,4,5,6,7,8,9. Decimal is also called base 10 because it has 10 digits. The reason why people started counting in decimal is because it has 10 digits and we have 10 fingers and people used to use their fingers for counting.

Binary

Binary uses only 2 digits which are 0 and 1 and is also called base 2. Binary is what computers use for counting because inside a computer you get things that are like little switches that can be either off or on(0 or 1). A subscripted 2 is placed after a binary number so that it can be recognised as being a binary number like in the following example:
1001₂
We already know that when we count we add 1 to the current number each time to get the next number. If we start at 0 and then add 1 we get 1. Now we have to add 1 to 1 but we have run out of digits because there are only 2 digits in binary. When we get to 9 in decimal and add 1 we first change the number to a 0 and then add 1 to the imaginary 0 to the left of it which gives us 10. If we apply this to binary then we change the 1 to 0 and then increase the imaginary 0 to the left of it which gives us 10 but this 10 is actually 2. The following sequence shows you how to count to 5 in binary:
0 1 10 11 100 101

Hexadecimal

The word hexadecimal is made up of 2 parts which are hex(6) and decimal(10). If you add 6 and 10 together you get 16 and that is how many digits there are in hexadecimal. Hexadecimal is sometimes called hex or base 16. To get 16 digits we have to use letters of the alphabet and those 16 digits are 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Hexadecimal is often used instead of binary numbers because just 2 hexadecimal digits can make the same numbers as 8 binary digits which in turn make up a byte. A subscripted 16 is used to show that a number is hexadecimal:
7F₁₆

Octal

Octal uses 8 digits which are 0,1,2,3,4,5,6,7 and is also called base 8. We use a subscripted 8 to show that a number is octal:
275₈

Converting from decimal to binary, hexadecimal and octal

decimal -> binary₂
5 -> binary₂
First write a few 2s(because it's base 2) to the power of the numbers 0,1,2,3,...
2³ 2² 2¹ 2⁰
Next calculate the values of these numbers.
8 4 2 1
The highest number must be greater than the number you want to convert.
Now divide the number to be converted by the number starting on the left. Write how many times the number divides into it underneath the number and then write your remainder on top of the next number to be divided. You then divide by the remainder each time after that.
5 5 1 1
8 4 2 1
0 1 0 1
The bottom line of numbers is the binary number. Make sure to leave out all leading 0s
5 -> 101₂
decimal -> hexadecimal₁₆
Decimal to hexadecimal works in the same way except that you use 16 to the power of those numbers since that is the base this time.
26 -> hexadecimal₁₆
16² 16¹ 16⁰
26 26 10
256 16 1
0 1 10
Before we write the answer we must change all numbers greater than 9 to their hexadecimal equivalents.
1 10
1 A
26 -> 1A₁₆
decimal -> octal₈
This time we use 8 to the power of those numbers because we are working with base 8.
12 -> octal₈
8² 8¹ 8⁰
12 12 4
64 8 1
0 1 4
12 -> 14₈

Converting from binary, hexadecimal and octal to decimal

binary₂ -> decimal
1101₂ -> decimal
First write 2 to the power of the numbers 0,1,2,3,...
2³ 2² 2¹ 2⁰
Now change them to their real values.
8 4 2 1
Now put the binary number underneath the other numbers and multiply the top number by the number beneath it and put the answer underneath the other 2 with + between each number and add the bottom row together to get your final answer.
8 4 2 1
1 1 0 1
8+4+0+1 = 13
1101₂ -> 13
hexadecimal₁₆ -> decimal
Once again you use 16 instead of 2.
1F₁₆ -> decimal
16¹ 16⁰
16 1
1 F
16+F = 16 + 15 = 31
1F₁₆ -> 31
octal₈ -> decimal
25₈ -> decimal
8¹ 8⁰
8 1
2 5
16+5 = 21
15₈ -> 21

Converting from hexadecimal to binary

hexadecimal₁₆ -> binary₂
2C₁₆ -> binary₂
First write the number as decimals.
2 12
Now divide each number by the numbers 8 4 2 1.
2    12
8421 8421
0010 1100
Take the leading 0s away and you have your answer.
2C₁₆ -> 101100₂
binary₂ -> hexadecimal₁₆
10111₂ -> hexadecimal₁₆
First separate the binary number into groups of 4 digits. If the number at the front has less than 4 digits then add 0s to the front of it.
0001 0111
Now use the numbers 8421 and multiply each time and add the results together for each group to get the answer.
0001 0111
8421 8421
0+0+0+1 = 1; 0+4+2+1 = 7
10111₂ -> 17₁₆

Converting from octal to binary

Octal to binary uses the same method as hexadecimal to binary except that you use the numbers 421 and groups of 3 digits.
octal₈ -> binary₂
26₈ -> binary₂
2   6
421 421
010 110
26₈ -> 10110₂
binary₂ -> octal₈
1010₂ -> octal₈
001 010
421 421
0+0+1 = 1; 0+2+0 = 2
1010₂ -> 12₈

Converting from hexadecimal to octal

We do not convert directly from hexadecimal to octal but instead first convert to binary and then to octal.
hexadecimal₁₆ -> octal₈
45₁₆ -> octal₈
First convert the hexadecimal number to binary.
4     5
8421 8421
0100 0101
Now make groups of 3 digits and then convert to octal.
001 000 101
421 421 421
0+0+1 = 1; 0+0+0 = 0; 4+0+1 = 5
45₁₆ -> 105₈
octal₈ -> hexadecimal₁₆
27₈ -> hexadecimal₁₆
First convert the octal number to binary.
2   7
421 421
010 111
Make groups of 4 and then convert to hexadecimal.
0001 0111
8421 8421
0+0+0+1 = 1; 0+4+2+1 = 7
27₈ -> 17₁₆

How to remember

All of these conversions follow certain patterns that you need to remember. When converting from decimal you always use divide and when converting to decimal you always multiply. Converting between hexadecimal and binary as well as octal and binary is a bit easier to remember. Just remember that hexadecimal is 8421 and octal is 421. The only thing you need to know about converting between hexadecimal and octal is that you must always convert to binary first.

Pascal Lesson 14 - Linked Lists

Learn Pascal Programming Tutorial Lesson 14 - Linked Lists

What is a linked list

A linked list is like an array except that the amount of elements in a linked list can change unlike an array. A linked list uses pointers to point to the next or previous element.

Single linked lists

There are 2 types of single linked lists which are called queues and stacks.

Queues

A queue is like standing in a queue at a shop. The first person that joins a queue is the first person to be served. You must always join at the back of a queue because if you join at the front the other people will be angry. This is called FIFO(First In First Out).
Item 1 --> Item 2 --> Item 3 --> (Until the last item)
Each item of a linked list is a record which has the data and a pointer to the next or previous item. Here is an example of how to declare the record for a queue and a pointer to a queue record as well as the variables needed:
program queue;

type
   pQueue = ^tqueue;
   tQueue = record
      data: integer;
      next: pQueue;
   end;

var
   head, last, cur: pQueue;

begin
end.
We will now make 3 procedures. The first procedure will add items to the list, the second will view the list and the third will free the memory used by the queue. Before we make the procedures lets first take a look at the main program.
begin
   head := nil; {Set head to nil because there are no items in the queue}
   add(1) {Add 1 to the queue using the add procedure};
   add(2);
   add(3);
   view; {View all items in the queue}
   destroy; {Free the memory used by the queue}
end.
The add procedure will take an integer as a parameter and add that integer to the end of the queue.
procedure add(i: integer);
begin
   new(cur); {Create new queue item}
   cur^.data := i; {Set the value of the queue item to i}
   cur^.next := nil; {Set the next item in the queue to nil because it doesn't exist}
   if head = nil then {If there is no head of the queue then}
      head := cur {Current is the new head because it is the first item being added to the list}
   else
      last^.next := cur; {Set the previous last item to current because it is the new last item in the queue}
   last := cur; {Make the current item the last item in the queue}
end;
The view procedure uses a loop to display the data from the first item to the last item of the queue.
procedure view;
begin
   cur := head; {Set current to the beginning of the queue}
   while cur <> nil do {While there is a current item}
      begin
         writeln(cur^.data); {Display current item}
         cur := cur^.next; {Set current to the next item in the queue}
      end;
end;
The destroy procedure will free the memory that was used by the queue.
procedure destroy;
begin
   cur := head; {Set current to the beginning of the queue}
   while cur <> nil do {While there is a item in the queue}
      begin
         cur := cur^.next; {Store the next item in current}
         dispose(head); {Free memory used by head}
         head := cur; {Set the new head of the queue to the current item}
      end;
end;

Stacks

To understand a stack you must think about a stack of plates. You can add a plate to the top of the stack and take one off the top but you can't add or take away a plate from the bottom without all the plates falling. This is called LIFO(Last In First Out).
Item 1 <-- Item 2 <-- Item 3 <-- (Until the last item)
When you declare the record for a stack item you must use previous instead of next. Here is an example.
program stack;

type
   pStack = ^tStack;
   tStack = record
      data: integer;
      prev: pStack;
   end;

var
   last, cur: pStack;

begin
   last := nil;
   add(3);
   add(2);
   add(1);
   view;
   destroy;
end.
You will see that the numbers are added from 3 to 1 with a stack instead of 1 to 3. This is because things must come off the top of the stack instead of from the head of a queue.
The add procedure adds the item after the last item on the stack.
procedure add(i: integer);
begin
   new(cur); {Create new stack item}
   cur^.data := i; {Set item value to the parameter value}
   cur^.prev := last; {Set the previous item to the last item in the stack}
   last := cur; {Make the current item the new last item}
end;
The view and destroy procedures are almost the same as with a queue so they will not need to be explained.
procedure view;
begin
   cur := last;
   while cur <> nil do
      begin
         writeln(cur^.data);
         cur := cur^.prev;
      end;
end;

procedure destroy;
begin
   while last <> nil do
      begin
         cur := last^.prev;
         dispose(last);
         last := cur;
      end;
end;

• Learn Pascal Programming Tutorial Lesson 1 - Introduction to Pascal
• Learn Pascal Programming Tutorial Lesson 2 - Colors, Coordinates, Windows and Sound
• Learn Pascal Programming Tutorial Lesson 3 - Variables and Constants
• Learn Pascal Programming Tutorial Lesson 4 - String Handling and Conversions
• Learn Pascal Programming Tutorial Lesson 5 - Decisions
• Learn Pascal Programming Tutorial Lesson 6 - Loops
• Learn Pascal Programming Tutorial Lesson 7 - Arrays
• Learn Pascal Programming Tutorial Lesson 8 - Types, Records and Sets
• Learn Pascal Programming Tutorial Lesson 9 - Procedures and Functions
• Learn Pascal Programming Tutorial Lesson 10 - Text Files
• Learn Pascal Programming Tutorial Lesson 11 - Data Files
• Learn Pascal Programming Tutorial Lesson 12 - Units
• Learn Pascal Programming Tutorial Lesson 13 - Pointers
• Learn Pascal Programming Tutorial Lesson 14 - Linked Lists

Pascal Lesson 13 - Pointers

Learn Pascal Programming Tutorial Lesson 13 - Pointers

What is a pointer?

A pointer is a type of variable that stores a memory address. Because it stores a memory address it is said to be pointing to it. There are 2 types of pointers which are typed and untyped. A typed pointer points to a variable such as an integer. An untyped pointer can point to any type of variable.

Declaring and using typed pointers

When you declare a typed pointer you must put a ^ in front of the variable type which you want it to point to. Here is an example of how to declare a pointer to an integer:
program Pointers;

var
   p: ^integer;

begin
end.
The @ sign can be used in front of a variable to get its memory address. This memory address can then be stored in a pointer because pointers store memory addresses. Here is an example of how to store the memory address of an integer in a pointer to an integer:
program Pointers;

var
   i: integer;
   p: ^integer;

begin
   p := @i;
end.
If you want to change the value stored at the memory address pointed at by a pointer you must first dereference the pointer variable using a ^ after the pointer name. Here is an example of how to change the value of an integer from 1 to 2 using a pointer:
program Pointers;

var
   i: integer;
   p: ^integer;

begin
   i := 1;
   p := @i;
   p^ := 2;
   writeln(i);
end.
You can allocate new memory to a typed pointer by using the new command. The new command has one parameter which is a pointer. The new command gets the memory that is the size of the variable type of the pointer and then sets the pointer to point to the memory address of it. When you are finished using the pointer you must use the dispose command to free the memory that was allocated to the pointer. Here is an example:
program Pointers;

var
   p: ^integer;

begin
   new(p);
   p^ := 3;
   writeln(p^);
   dispose(p);
end.

Declaring and using untyped pointers

When you declare an untyped pointer you must use the variable type called pointer.
program Pointers;

var
   p: pointer;

begin
end.
When you allocate memory to an untyped pointer you must use the getmem command instead of the new command and you must use freemem instead of dispose. getmem and freemem each have a second parameter which is the size in bytes of the amount of memory which must be allocated to the pointer. You can either use a number for the size or you can use the sizeof function to get the size of a specific variable type.
program Pointers;

var
   p: pointer;

begin
   getmem(p,sizeof(integer));
   freemem(p,sizeof(integer));
end.

• Learn Pascal Programming Tutorial Lesson 1 - Introduction to Pascal
• Learn Pascal Programming Tutorial Lesson 2 - Colors, Coordinates, Windows and Sound
• Learn Pascal Programming Tutorial Lesson 3 - Variables and Constants
• Learn Pascal Programming Tutorial Lesson 4 - String Handling and Conversions
• Learn Pascal Programming Tutorial Lesson 5 - Decisions
• Learn Pascal Programming Tutorial Lesson 6 - Loops
• Learn Pascal Programming Tutorial Lesson 7 - Arrays
• Learn Pascal Programming Tutorial Lesson 8 - Types, Records and Sets
• Learn Pascal Programming Tutorial Lesson 9 - Procedures and Functions
• Learn Pascal Programming Tutorial Lesson 10 - Text Files
• Learn Pascal Programming Tutorial Lesson 11 - Data Files
• Learn Pascal Programming Tutorial Lesson 12 - Units
• Learn Pascal Programming Tutorial Lesson 13 - Pointers
• Learn Pascal Programming Tutorial Lesson 14 - Linked Lists